Tucker Dooley

I went to the Purdue Corn maze with some friends, and the corn maze has numerous coupon stations scattered throughout the maze. I figured it would be an interesting problem to try making a program that would find the shortest path from the start, through all the coupon stations, and back to the start. I later realized that this is literally just the "Traveling Salesman Problem".

I decided to use Python for simplicity. I start by reading in a maze.png and converting it to binary (0,1) pixel values using a threshhold value to compare the pixels against. Then I added all the white pixels to an adj list. Then I wrote a BFS and an A* function to find the shortest paths between 2 points. Then to find the shortest route, I calculated the shortest distance from every point to every other point ( with the exceptions of the start and end points ). Then once the shortest paths are stored I can do the brute force traveling salesman algorithm where I consider every permutation of paths through the points. This has N! time complexity, but since all the paths are already computed it doesn't take very long. I plan to eventually use the dynamic programming traveling salesman approach to improve time efficiency.

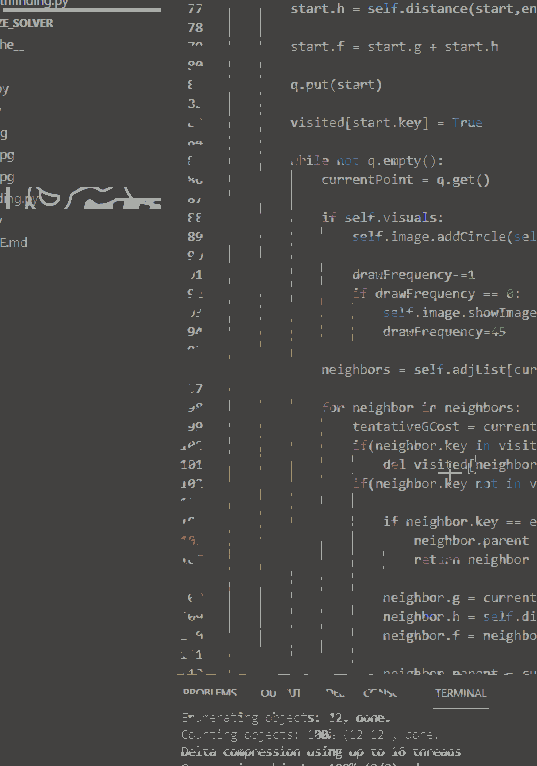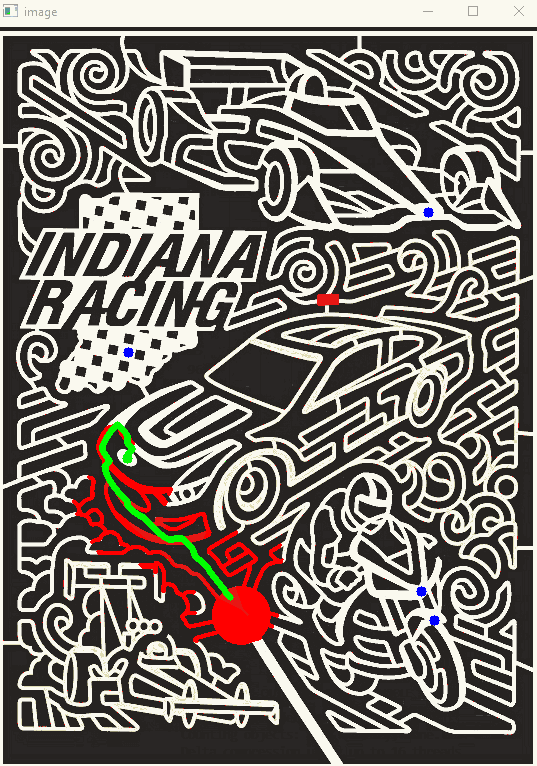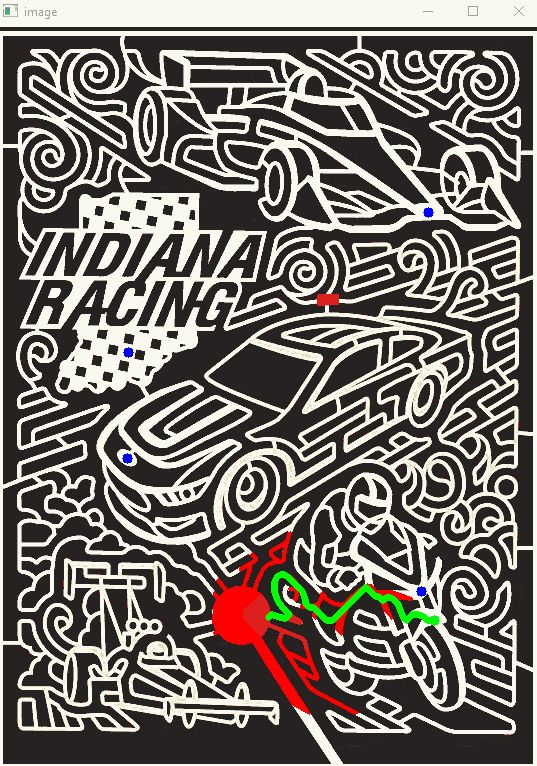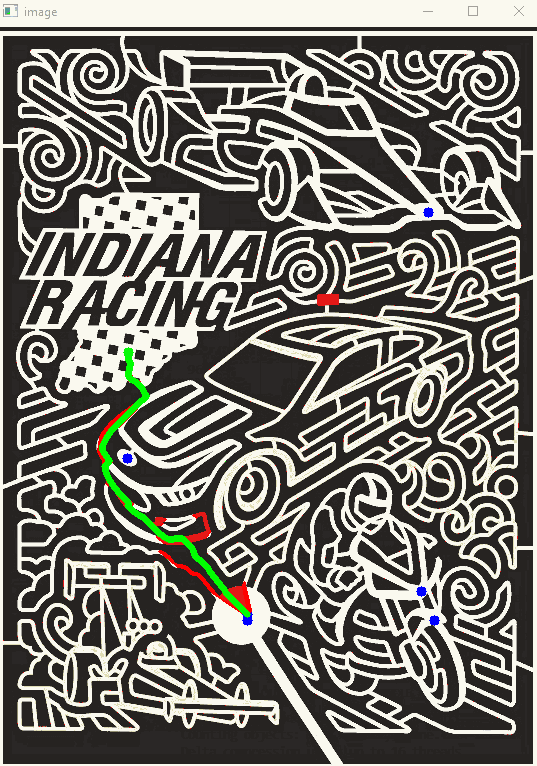
For fun I programmed some visualizations of the pathfinding process. I programmed in a delay so we can slowly watch the pathfinding process. Below are some GIF's demonstrating this.

The first is A*, the second is BFS, the last image is the resulting shortest path. Except the resulting path does not return to the start yet.